Autor: Krzysztof

ZPO2017-w12.pdf

W związku z pytaniami informuję, że laboratoria ZPO w styczniu odbywają się wg harmonogramu przedstawionego w ogłoszeniu z 30 października 2017, niezależnie od tego, jaka kolejność grup jest zapisana w USOSie.

Przy okazji przypominam, że 23 stycznia i 24 stycznia odbędą się zajęcia nr 8 wspólne dla grup parzystych i nieparzystych, na które przychodzą tylko te osoby, które chcą anulować jedną ze swoich ocen (np. zero, ale niekoniecznie – można też chcieć zamienić inną ocenę) i zastąpić ją oceną zdobytą na tych zajęciach.

Zadania, które dotyczą zakresu materiału, jaki będzie poruszany na lab. 7. Rozwiązanie nie jest wymagane. Zadania stanowią wyłącznie pomoc w przygotowaniu się do zajęć.

Założenia

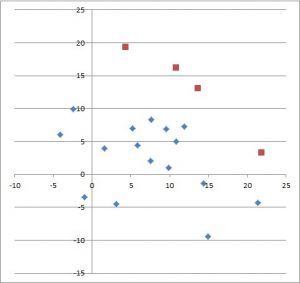
Przyjmijmy, że mamy zbiór punktów w przestrzeni n-wymiarowej, przy czym współrzędne pojedynczego punktu są reprezentowane w postaci wektora liczb rzeczywistych o długości n. Mówimy, że punkt A dominuje nad punktem B, jeżeli dla każdej współrzędnej A(i) odpowiadająca jej współrzędna B(i) jest mniejsza lub równa, oraz istnieje co najmniej jedna taka współrzędna j dla której A(j)>B(j). Można też wtedy powiedzieć, że B jest zdominowane przez A. Jeżeli natomiast dla pary punktów taki warunek nie jest spełniony, tj. ani A nie dominuje nad B, ani B nad A, wtedy uważamy punkty A i B za nieporównywalne względem siebie. W zbiorze punktów punkt niezdominowany to taki, który może tylko dominować lub być nieporównywalnym z wszystkimi pozostałymi punktami.

Zadanie 1

Wygeneruj zbiór 100 losowych punktów w przestrzeni n-wymiarowej, po czym znajdź w nim zbiór punktów niezdominowanych. Algorytm znajdowania punktów niezdominowanych polega na porównaniu każdego punktu ze wszystkimi pozostałymi (nie dokonujemy porównania punktu z samym sobą). Jeżeli dla aktualnie sprawdzanego punktu z żadnego porównania nie wyniknie, że jest zdominowany, to znaczy, że jest niezdominowany. Znaleziony punkt niezdominowany należy zapisać w kontenerze pomocniczym. Na koniec sprawdzania kontener pomocniczy zawiera wyłącznie punkty niezdominowane.
Algorytm można zrealizować z pomocą dwóch kontenerów zawierających zestawy tych samych 100 punktów oraz kontenera pomocniczego, który początkowo jest pusty. Punkty z pierwszego kontenera są punktami sprawdzanymi, a punkty z drugiego – punktami z którymi dokonywane jest sprawdzenie. Do kontenera pomocniczego trafiają kopie tych punktów z kontenera pierwszego, które okazały się niezdominowane. Realizacja czynności odbywa się za pomocą dwóch pętli for – zewnętrznej (punkty z pierwszego kontenera) i wewnętrznej (punkty z drugiego kontenera).
Po zaimplementowaniu algorytmu spróbuj zaimplementować go ponownie, ale tym razem bez używania pętli for, natomiast stosując algorytmy STL oraz własne lub biblioteczne obiekty funkcyjne. Sprawdź, czy uzyskałeś ten sam wynik.

Zadanie 2

Wygeneruj zbiór 100 punktów losowo rozłożonych na okręgu o promieniu 1 (Algorytm 2), po czym znajdź w nim zbiór punktów niezdominowanych. W kontenerze uporządkuj rosnąco niezdominowane punkty pod względem ich pierwszej współrzędnej. Wykorzystując algorytm adjacent_difference (slajdy 120 i 121, wykład 11) policz odległości euklidesowe miedzy sąsiednimi punktami (tj. między punktami 1 i 2, 2 i 3, 3 i 4, itd.). W obiekcie funkcyjnym służącym do obliczenia odległości euklidesowej miedzy dwoma punktami skorzystaj z algorytmu inner_product, tak jak to jest pokazane na slajdzie 119 wykładu 11. Policzone odległości zapisz do pomocniczego kontenera, a na koniec policz średnią odległość między punktami oraz wariancję tej odległości.
Przy pisaniu kodu programu unikaj pętli for, a zamiast niej stosuj algorytmy STL oraz własne lub biblioteczne obiekty funkcyjne.

ZPO2017-w11.pdf

ZPO2017-w10.pdf

Zadania, które dotyczą zakresu materiału, jaki będzie poruszany na lab. 6. Rozwiązanie nie jest wymagane. Zadania stanowią wyłącznie pomoc w przygotowaniu się do zajęć.

Zadanie 1:

Przyjmij, że A, B, C i D reprezentują punkty w przestrzeni n-wymiarowej. Punkty te są reprezentowane w programie przez wektory współrzędnych. Wektor A zawiera dla każdej współrzędnej uzyskaną niezależnie wartość losową o rozkładzie jednostajnym z przedziału [-10,10]. Wektor B zawiera [1,..,1].

Pobierz od użytkownika liczbę wymiarów przestrzeni n, utwórz odpowiednich rozmiarów wektory, przy czym zainicjuj też odpowiednio A i B, a następnie wykonaj w programie kolejno następujące obliczenia:

1. D = A*B
2. C = 3*B + D
3. D = 3*(A+C)-(A*B)

Gdzie operator '*’ oznacza mnożenie, przy czym kiedy argumentami są skalar i wektor, następuje przemnożenie wszystkich współrzędnych wektora przez skalar, natomiast w przypadku, kiedy argumentami są dwa wektory, jest to iloczyn Hadamarda (zobacz: https://pl.wikipedia.org/wiki/Mnożenie_macierzy). Sprawdź na danych testowych, czy obliczenia wykonują się poprawnie.

Uwaga: do zaimplementowania w/w operacji nie wykorzystuj żadnych pętli (for, while, repeat), a wyłącznie algorytmy STL i obiekty funkcyjne (własne lub biblioteczne). Jeżeli to potrzebne, rozłóż operacje na pojedyncze kroki, których wynik zapamiętuj w wektorach pomocniczych.

Zadanie 2:

W celu wygenerowania punktu na powierzchni hipersfery (zobacz: https://pl.wikipedia.org/wiki/Hipersfera) z centrum w środku układu współrzędnych należy wykonać następujące kroki:

1. wygenerować wektor Z, którego każda współrzędna jest uzyskaną niezależnie wartością losową z generatora liczb o rozkładzie normalnym. Liczba współrzędnych wektora odpowiada liczbie wymiarów przestrzeni, w której definiowana jest hipersfera,
2. policzyć ||Z||, tj. długość wektora Z, a następnie podzielić każdą ze współrzędnych wektora Z przez tę długość.

Nowy wektor Z reprezentuje punkt na powierzchni hipersfery o promieniu 1 z centrum w środku układu współrzędnych.

Wygeneruj wiele takich punktów dla przestrzeni 2-wymiarowej i przedstaw je w postaci graficznej. Sprawdź, czy układają się w kształt okręgu.

Uwaga: do zaimplementowania w/w operacji nie wykorzystuj żadnych pętli (for, while, repeat), a wyłącznie algorytmy STL i obiekty funkcyjne (własne lub biblioteczne). Jeżeli to potrzebne, rozłóż operacje na pojedyncze kroki, których wynik zapamiętuj w wektorach pomocniczych.

ZPO2017-w9.pdf

ZPO2017-w8.pdf